class: center, middle, inverse, title-slide # Outcome regression and propensity scores ## What If: Chapter 15 ### Elena Dudukina ### 2021-12-08 --- # Introduction - Non-g(generalized) methods, e.g. outcome regression and propensity score-based methods don't work in a complex scenario with time-varying treatments --- # 15.1 Outcome regression - Our causal contrast of interest: - `\(E[Y^{a=1, c=0}] - E[Y^{a=0, c=0}]\)` or in words, the risk difference (average causal effect) under exposure level a=1 as compared with the same population under exposure level a=0 had no one been censored and in the absense of the sources of the systematic errors - Our assumptions: - The exposed and non-exposed are exhangeable given confounders L: - `\(Y^a \perp\perp A|L]\)` - Exposure consistency assumption, or the exposure variants are irrelevant (well-defined intervention) - Positivity assumption (we observe exposed and unexposed in every level of every confounder) - No interferance (the potential outcome in one participant is independent of the exposure level of another participant) --- # 15.1 Outcome regression - G-methods: IPT weighting, standardization (parametric g-formula), g-estimation - Consider structural model: - `\(E[Y^{a, c=0}|L] = \beta_0 + \beta_1a + \beta_2aL + \beta_3L\)` - average causal effect of A on Y in each stratum of L is the function of `\(\beta_1\)` and `\(\beta_2\)` - the average causal effect of A on Y under no treatment (a=0) in each stratum of L is the function of `\(\beta_0\)` and `\(\beta_3\)` - suggesting that `\(\beta_3\)` is the causal effect of L is "table 2 fallacy" - Given all assumptions hold, we can estimate the desired contrast (parameters of the structural model) using outcome regression: - `\(E[Y|A, C=0, L] = \alpha_0 + \alpha_1A + \alpha_2AL + \alpha_3L\)` - adjustment estimates causal effects in each stratum of L - in unbiased situation, parameters `\(\beta\)` are the same as `\(\alpha\)` are the same - we computed conditional effect estimated (since we did not standardize over L as in g-formula or IPTW approaches) --- # 15.1 Outcome regression .panelset[ .panel[.panel-name[Code] ```r library(tidyverse) library(magrittr) # getting the data data <- readr::read_csv(file = "https://cdn1.sph.harvard.edu/wp-content/uploads/sites/1268/1268/20/nhefs.csv") %>% mutate( education = case_when( education == 1 ~ "8th grade or less", education == 2 ~ "HS dropout", education == 3 ~ "HS", education == 4 ~ "College dropout", education == 5 ~ "College or more", T ~ "missing" ) ) %>% mutate(across(.cols = c(sex, race, education, exercise, active), .fns = forcats::as_factor)) %>% drop_na(qsmk, sex, race, education, exercise, active, wt82) ``` ] .panel[.panel-name[Data] ```r # what's inside? data %>% select(qsmk, age, sex, race, education, wt71, smokeintensity, smokeyrs, exercise, active) ``` ``` ## # A tibble: 1,566 x 10 ## qsmk age sex race education wt71 smokeintensity smokeyrs exercise ## <dbl> <dbl> <fct> <fct> <fct> <dbl> <dbl> <dbl> <fct> ## 1 0 42 0 1 8th grade or ~ 79.0 30 29 2 ## 2 0 36 0 0 HS dropout 58.6 20 24 0 ## 3 0 56 1 1 HS dropout 56.8 20 26 2 ## 4 0 68 0 1 8th grade or ~ 59.4 3 53 2 ## 5 0 40 0 0 HS dropout 87.1 20 19 1 ## 6 0 43 1 1 HS dropout 99 10 21 1 ## 7 0 56 1 0 HS 63.0 20 39 1 ## 8 0 29 1 0 HS 58.7 2 9 2 ## 9 0 51 0 0 HS dropout 64.9 25 37 2 ## 10 0 43 0 0 HS dropout 62.3 20 25 2 ## # ... with 1,556 more rows, and 1 more variable: active <fct> ``` ]] --- # Otcome regression ## Fitting the model ```r # fit a regression of the outcome on the exposure and confounders fit <- glm(data = data, formula = wt82_71 ~ qsmk + sex + race + age + I(age*age) + education + smokeintensity + I(smokeintensity*smokeintensity) + smokeyrs + I(smokeyrs*smokeyrs) + exercise + active + wt71 + I(wt71*wt71), family = gaussian()) fit %>% broom::tidy(conf.int = T) %>% filter(term == "qsmk") ``` ``` ## # A tibble: 1 x 7 ## term estimate std.error statistic p.value conf.low conf.high ## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 qsmk 3.46 0.438 7.90 5.36e-15 2.60 4.32 ``` ```r # Hernan: model without any product terms yielded the estimate 3.5 (95% confidence interval: 2.6, 4.3) kg. ``` --- # 15.2 Propensity scores - When using [IPT-weigting](https://whatif-kea-book-club-chapter12.netlify.app/) or [g-estimation](https://whatif-kea-book-club-chapter14.netlify.app/), we computed the exposure probability given the covariables `\(Pr[A=1|L]\)` at an individual level in the dataset - `\(\tau(L)\)` is the propensity score - `\(\tau(L)\)` is a conditional probability of exposure given covariables - `\(\tau(L)\)` is close to 0 for those with low treatment probabaility and close to 1 among those with high probability of the exposure - in the ideal randomized trial (with the randomization probability of 0.5), the `\(\tau(L)\)` would be 0.5 for all individuals - in an observational study the true `\(\tau(L)\)` is unknown and needs to be estimated from the data --- # 15.2 Propensity scores .panelset[ .panel[.panel-name[Estimating PS] ```r fit <- glm(qsmk ~ sex + race + age + I(age*age) + education + smokeintensity + I(smokeintensity*smokeintensity) + smokeyrs + I(smokeyrs*smokeyrs) + exercise + active + wt71 + I(wt71*wt71), data = data, family = binomial()) data %<>% mutate( ps = predict(fit, type = "response", newdata = .) ) ``` ] .panel[.panel-name[PS histogram] ```r data %>% ggplot(aes(x = ps, color = as.factor(qsmk), fill = as.factor(qsmk))) + geom_histogram(alpha = 0.2, bins = 30) + # facet_grid(rows = vars(qsmk)) + theme_minimal(base_size = 12)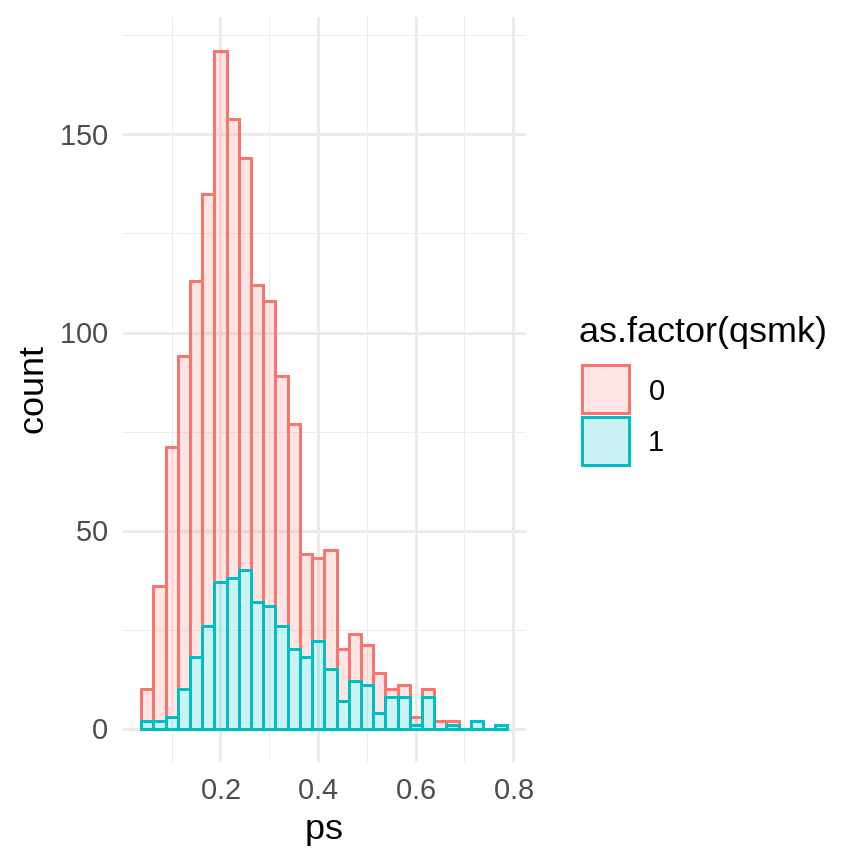 ``` <img src="index_files/figure-html/unnamed-chunk-6-1.png" width="288" /> ] .panel[.panel-name[PS density plot] ```r data %>% ggplot(aes(x = ps, color = as.factor(qsmk), fill = as.factor(qsmk))) + geom_density(alpha = 0.2) + # facet_grid(rows = vars(qsmk)) + theme_minimal(base_size = 12)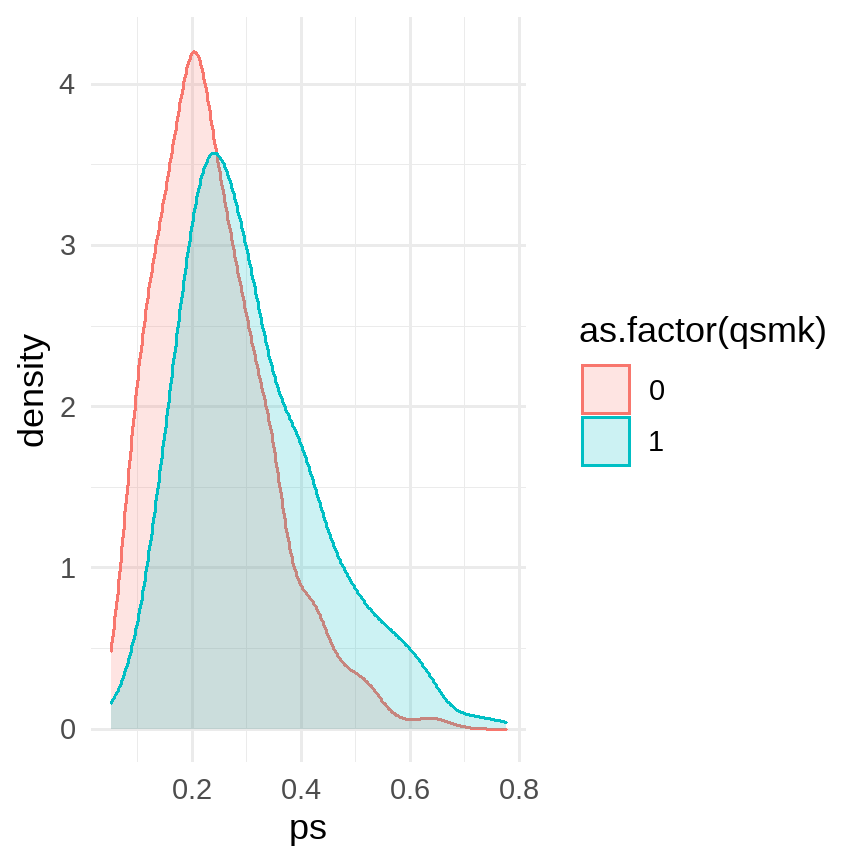 ``` <img src="index_files/figure-html/unnamed-chunk-7-1.png" width="288" /> ] .panel[.panel-name[PS summary] ```r data %>% group_by(qsmk) %>% summarise(min = min(ps), mean = mean(ps), median = median(ps), max = max(ps)) ``` ``` ## # A tibble: 2 x 5 ## qsmk min mean median max ## <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 0 0.0510 0.239 0.222 0.681 ## 2 1 0.0599 0.309 0.282 0.777 ``` ] .panel[.panel-name[Fitting outcome regression model with PS as a covariable] ```r fit <- glm(data = data, formula = wt82_71 ~ qsmk + ps) %>% broom::tidy(conf.int = T) ``` ] .panel[.panel-name[Outcome regression model with PS as a covariable] ```r fit %>% filter(term == "qsmk") ``` ``` ## # A tibble: 1 x 7 ## term estimate std.error statistic p.value conf.low conf.high ## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> ## 1 qsmk 3.45 0.460 7.52 9.41e-14 2.55 4.35 ``` ```r # Hernan: model without any product terms yielded the estimate 3.5 (95% confidence interval: 2.6, 4.3) kg. ``` ]] --- # 15.2 Propensity scores - Smoking stoppers had higher PS than non-stoppers - Individuals with the same propensity score values have different values of different covariables - PS is a balancing score - The of PS-based methods (IPTW, stratification, matching) still requires all causal assumptions (exchangeability given measured covariables, consistency, positivity, and no interference) - Conditional exchangeability: `\(Y^a \perp \perp A = |L\)` = `\(Y^a \perp \perp A = |\tau(L)\)` - Positivity: no individual had a PS of 0 or 1 --- # 15.3 Propensity stratification and standardizaion - Low chances that `\(\tau(L)\)` will have the same value for two participants (continuous variable) - Strata with similar although not the same values of `\(\tau(L)\)` (eg deciles) --> potential lack of exchangeability between treated and untreated in some strata - Fitting an outcome regression model with PS as a covariable - Validity: causal assumptions and correct specification of the model Y ~ `\(\tau(L)\)` (while IPTW is agnostic about this relation) - Estimating the causal effect in each stratum and standardizing along the PS distribution to compute average causal effect --- # 15.4 Propensity matching - Under exchangeability and positivity given PS, associations in the matched population (matched pairs) are consistently estimating the associations in the whole population - Exact matching is not effective - Matching based on some value of closeness (s=0.05 or similar). - If the closeness criterion is loose, the exchangeability between treated and untreated will be lost in the matched population - If the closeness criterion is too tight, the exchangeability will hold but precision will be lost - Unlike outcome regression with PS, the PS matching does not distinguish between random and structural non-positivity - Matching may exclude treated with no matches among untreated --> initial and matched populations are not the same and the estimated effect is not average causal effect but average causal effect in the treated - No clear view of who was excluded since propensity score value does not translate into patients characteristics straightforwardly - Transportability of the effect measure computed for the matched population? --- # 15.5 Propensity models, structural models, predictive models - Aim of the study dictates what methods to use: causal or predictive - Variable selection for answering causal questions is different from that when interested in a predictive task --- # References 1. Hernán MA, Robins JM (2020). Causal Inference: What If. Boca Raton: Chapman & Hall/CRC (v. 30mar21)